На этом уроке мы будем изучать первый признак равенства треугольников. Вначале сформулируем и докажем теорему о первом признаке равенства треугольников. Далее будем решать задачи на использование первого признака равенства треугольников.

На предыдущем занятии мы ввели понятие «равные треугольники» - треугольники, которые можно совместить наложением. Однако очень трудно сравнивать фигуры по определению, поэтому мы введем признаки равенства треугольников - по некоторым элементам.

Рис. 1. Треугольники АВС и A 1 B 1 C 1 равны

Докажем теорему: если две стороны и угол между ними одного треугольника и соответствующие им две стороны и угол между ними второго треугольника равны, то данные треугольники равны.

Теорема: Дано . Доказать: АВС и .

Доказательство: Выполним наложение данных в условии фигур. В результате данного действия вершины А и А 1 , отрезки АВ и А 1 В 1, АС и А 1 С 1 совпадают. Если рассматривать треугольники в целом, то совпадёт с .

Теорема доказана.

Рассмотрим несколько задач.

Отрезки АС и ВD точкой их пересечения О делятся пополам. Докажите, что .

Доказательство: Выполним пояснительный рисунок.

Рис. 2. Чертеж к примеру 1

Отметим, что углы АОВ и СОD равны, как вертикальные, а стороны ВО и АО треугольника АОВ соответственно равны сторонам OD и ОС треугольника СОD. Поэтому треугольники АОВ и СОD равны по первому признаку.

Отрезки АС и BD точкой пересечения делятся пополам. Докажите, что .

Рис. 3. Чертеж к примеру 2

В предыдущей задаче мы доказали, что по первому признаку. Из этих соображений мы можем сделать вывод, что AB = CD, ∠OAB = ∠OCD.

Теперь рассмотрим треугольники. У них АС - общая сторона, AB=CD, а ∠СAB = ∠АCD (по доказанному). Поэтому по первому признаку равенства. Что и требовалось доказать.

Рис. 4. Чертеж к примеру 3

На рисунке 3 отрезки АВ и АС равны. Угол 1 равен углу 2. Известно, что АС = 15 см, DC = 5 см. Доказать, что . Найдите длины отрезков BD и АВ.

Треугольники равны по первому признаку, ведь ∠1 = ∠2, АВ = АС, а AD - общая сторона у обоих треугольников. Из равенства треугольников следует равенство некоторых их соответствующих элементов, поэтому: BD = CD = 5 см,

АВ = АС = 15 см.

Ответ: 5 см, 15 см.

На рисунке 5 ВС = AD. Угол 1 равен углу 2, AD = 17 см, CD = 14 см. Доказать, что . Найдите АВ и ВС.

Рис. 5. Чертеж к примеру 4

Треугольник АВС равен треугольнику СDА. по первому признаку. ∠1 = ∠2, СВ = АD, а AC - общая сторона у обоих треугольников. Из этого следует, что , .

1. Тема урока "Первый признак равенства треугольников"
2. Треугольник. Справочник

1. № 36. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. - М.: Просвещение, 2010.

2. Докажите, что треугольники ВОА и ЕОС равны. Отрезки ВЕ и AС точкой пересечения делятся пополам.

3. Докажите, что прямая, отсекающая от сторон угла равные отрезки, перпендикулярна его биссектрисе.

4. *На сторонах угла М отложены равные отрезки МА и МС и проведена его биссектриса, на которой отмечена точка В. Докажите, что ВМ является биссектрисой угла АВС.

При решении геометрических задач полезно следовать такому алгоритму. Во время чтения условия задачи необходимо

• Сделать чертеж. Чертеж должен максимально соответствовать условию задачи, так его основная задача помочь найти ход решения
• Нанести все данные из условия задачи на чертеж
• Выписать все геометрические понятия, которые встречаются в задаче
• Вспомнить все теоремы, которые относятся к этим понятию
• Нанести на чертеж все соотношения между элементами геометрической фигуры, которые следуют из этих теорем

Например, если в задаче встречается слова биссектриса угла треугольника, нужно вспомнить определение и свойства биссектрисы и обозначить на чертеже равные или пропорциональные отрезки и углы.

В этой статье вы найдете основные свойства треугольника, которые необходимо знать для успешного решения задач.

ТРЕУГОЛЬНИК.

Площадь треугольника.

1. ,

здесь - произвольная сторона треугольника, - высота, опущенная на эту сторону.

2. ,

здесь и - произвольные стороны треугольника, - угол между этими сторонами:

3. Формула Герона:

Здесь - длины сторон треугольника, - полупериметр треугольника,

4. ,

здесь - полупериметр треугольника, - радиус вписанной окружности.

Пусть - длины отрезков касательных.

Тогда формулу Герона можно записать в таком виде:

5.

6. ,

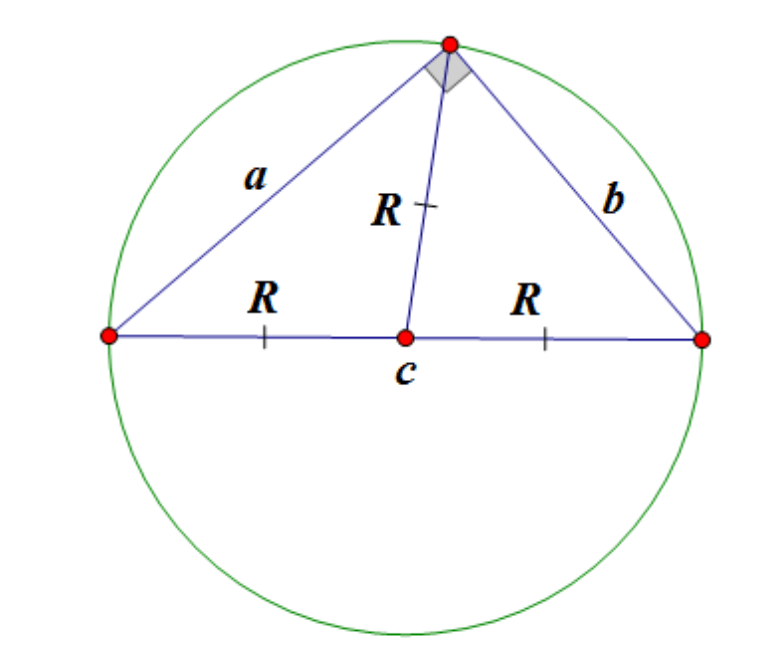
здесь - длины сторон треугольника, - радиус описанной окружности.

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Медиана треугольника

Это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

Радиус описанной окружности в два раза больше радиуса вписанной окружности: R=2r

Длина медианы произвольного треугольника

,

здесь - медиана, проведенная к стороне , - длины сторон треугольника.

Биссектриса треугольника

Это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.

Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:

Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.

Все точки биссектрисы угла равноудалены от сторон угла.

Высота треугольника

Это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Чтобы найти высоту треугольника , проведенную к стороне , нужно любым доступным способом найти его площадь, а затем воспользоваться формулой:

Центр окружности, описанной около треугольника , лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.

Радиус описанной окружности треугольника можно найти по таким формулам:

Здесь - длины сторон треугольника, - площадь треугольника.

,

где - длина стороны треугольника, - противолежащий угол. (Эта формула вытекает из теоремы синусов).

Неравенство треугольника

Каждая сторона треугольника меньше суммы и больше разности двух других.

Сумма длин любых двух сторон всегда больше длины третьей стороны:

Напротив большей стороны лежит больший угол; напротив большего угла лежит большая сторона:

Если , то и наоборот.

Теорема синусов:

стороны треугольника пропорциональны синусам противолежащих углов:

Теорема косинусов:

квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

Прямоугольный треугольник

- это треугольник, один из углов которого равен 90°.

Сумма острых углов прямоугольного треугольника равна 90°.

Гипотенуза - это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.

Теорема Пифагора:

квадрат гипотенузы равен сумме квадратов катетов :

Радиус окружности, вписанной в прямоугольный треугольник, равен

,

здесь - радиус вписанной окружности, - катеты, - гипотенуза:

Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:

Медиана прямоугольного треугольника, проведенная к гипотенузе , равна половине гипотенузы.

Определение синуса, косинуса, тангенса и котангенса прямоугольного треугольника смотрите

Соотношение элементов в прямоугольном треугольнике:

Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:

Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:

Катет, лежащий против угла равен половине гипотенузы:

Равнобедренный треугольник.

Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.

В равнобедренном треугольнике углы при основании равны.

Угол при вершине.

И - боковые стороны,

И - углы при основании.

Высота, биссектриса и медиана.

Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.

Правильный треугольник

(или равносторонний треугольник ) - это треугольник, все стороны и углы которого равны между собой.

Площадь правильного треугольника равна

где - длина стороны треугольника.

Центр окружности, вписанной в правильный треугольник , совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.

Средняя линия треугольника

Это отрезок, соединяющий середины двух сторон.

На рисунке DE - средняя линия треугольника ABC.

Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE

Внешний угол треугольника

Это угол, смежный какому либо углу треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Тригонометрические функции внешнего угла:

Признаки равенства треугольников:

1 . Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2 . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.

Признаки подобия треугольников:

1 . Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.

2 . Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.

3 . Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.

Важно: в подобных треугольниках сходственные стороны лежат против равных углов.

Теорема Менелая

Пусть прямая пересекает треугольник , причем – точка ее пересечения со стороной , – точка ее пересечения со стороной , и – точка ее пересечения с продолжением стороны . Тогда

1) по двум сторонам и углу между ними

Доказательство:

Пусть у треугольников АВС и А 1 В 1 С 1 угол A равен углу А 1 , АВ равно А 1 В 1, АС равно А 1 С 1 . Докажем, что треугольники равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A 1 B 1 C 1 так, чтобы угол A совместился с углом A 1 . Так как АВ=А 1 В 1 , а АС=А 1 С 1 , то B совпадёт с В 1 , а C совпадёт с С 1. Значит, треугольник А 1 В 1 С 1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

2) по стороне и прилежащим к ней углам

Доказательство:

ПустьАВС и А 1 В 1 С 1 - два треугольника, у которых АВ равно А 1 В 1, угол А равен углу А 1 , и угол В равен углу В 1 . Докажем, что они равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A 1 B 1 C 1 так, чтобы AB совпало с A 1 B 1. Так как ∠ВАС =∠В 1 А 1 С 1 и ∠АВС=∠А 1 В 1 С 1 , то луч АС совпадёт с А 1 С 1 , а ВС совпадёт с В 1 С 1 . Отсюда следует, что вершина C совпадёт с С 1. Значит, треугольник А 1 В 1 С 1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

3) по трём сторонам

Доказательство :

Рассмотрим треугольники ABC и A l B l C 1, у которых АВ=А 1 В 1 , BC = B l C 1 СА=С 1 А 1. Докажем, что ΔАВС =ΔA 1 B 1 C 1 .

Приложим треугольник ABC (либо симметричный ему) к треугольнику A 1 B 1 C 1 так, чтобы вершина А совместилась с вершиной A 1 , вершина В — с вершиной В 1 , а вершины С и С 1 , оказались по разные стороны от прямой А 1 В 1 . Рассмотрим 3 случая:

1) Луч С 1 С про-ходит внутри угла А 1 С 1 В 1 . Так как по условию теоремы стороны АС и A 1 C 1 , ВС и В 1 С 1 равны, то треугольники A 1 C 1 C и В 1 С 1 С — равнобедренные . По теореме о свойстве углов равнобедренного треугольника ∠1 = ∠2, ∠3 = ∠4, поэтому ∠ACB=∠A 1 C 1 B 1 .

2) Луч С 1 С совпадает с одной из сторон этого угла. A лежит на CC 1 . AC=A 1 C 1 , BC=B 1 C 1 , C 1 BC - равнобедренный , ∠ACB=∠A 1 C 1 B 1 .

3) Луч C 1 C проходит вне угла А 1 С 1 В 1 . AC=A 1 C 1 , BC=B 1 C 1 , значит, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1 .

Итак, AC=A 1 C 1 , BC=B 1 C 1 , ∠C=∠C 1 . Следовательно, треугольники ABC и A 1 B 1 C 1 равны по
первому признаку равенства треугольников.

Теорема доказана.

2. Деление отрезка на n равных частей.

Провести луч через A, отложить на нём n равных отрезков. Через B и A n провести прямую и к ней параллельные через точки A 1 - A n -1. Отметим их точки пересечения с AB. Получим n отрезков, которые равны по теореме Фалеса.

Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Доказательство. AB=CD

1. Проведём через точки A и C прямые, параллельные другой стороне угла. Получим два параллелограмма AB 2 B 1 A 1 и CD 2 D 1 C 1 . Согласно свойству параллелограмма : AB 2 = A 1 B 1 и CD 2 = C 1 D 1 .

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 и равны на основании второго признака равенства треугольников:
AB = CD согласно условию теоремы,
как соответственные, образовавшиеся при пересечении параллельных BB 1 и DD 1 прямой BD.

3. Аналогично каждый из углов и оказывается равным углу с вершиной в точке пересечения секущих. AB 2 = CD 2 как соответственные элементы в равных треугольниках.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

В этой статье мы расскажем, как можно сформулировать и доказать первый признак равенства треугольников , который проходят в 7 классе.

Формулировка первого признака равенства треугольников

«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»

Сокращенно его называют равенство «по двум сторонам и углу между ними».

Прежде чем перейти к необходимо вспомнить, что называют треугольником и в каком случае можно утверждать, что два треугольника равны.

Что такое треугольник и когда они считаются равными?

Треугольник – это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии, что они не лежат на одной прямой. Эти точки считаются вершинами треугольника. А соединяющие их отрезки – сторонами ).

На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.

Рисунок 1

Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными ). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.

Доказательство первого признака равенства треугольников

Дано:

Два треугольника: ABC и DEF (рисунок 2).

Рисунок 2

По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).

Доказать , что треугольник ABC равен треугольнику DEF.

Доказательство:

1. Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
2. При этом отрезки СА и СВ наложатся на отрезки FE и FD.
3. А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
4. Это в свою очередь даст совмещение вершин А и D, В и Е.
5. Следовательно, треугольники полностью совместятся, а значит, они равны.

Теорема доказана.

Билет 2

Вопрос 1

Признаки равенства треугольников (доказательство всех)

1-ый признак равенства треугольников: по двум сторонам и углу между ними (Теорема 3.1. – Признак равенства треугольников по двум сторонам и углу между ними - Если две стороны и угло между ними одного треугольнгрка равны соотвественно двум сторонам и углу между ними другого треугольника, то такие треугольники равны )

Доказательство:

Пусть у треугольников АВС и А 1 В 1 С 1 угол А равен углу А 1 , АВ равно А 1 В 1, АС равно А 1 С 1 , докажем, что треугольники равны.

Так как А 1 В 1 равно А 1 В 2 , то вершина В 2 совпадет с В 1. Так как угол В 1 А 1 С 1 равен углу В 2 А 1 С 2, то луч А 1 С 2 совпадет с А 1 С 1 . Так как А 1 С 1 равен А 1 С 2 , то С 2 совпадет с С 1. Значит треугольник А 1 В 1 С 1 совпадает стреугольниом А 1 В 2 С 2 , значит равен треугльнику АВС.

Теорема доказана.

2-ой признак равенства треугольников: по стороне и прилежим к ней углам (Теорема 3.2. - Признак равенства треугольников по стороне и прилежащим к ней углам - Если сторона и прилежащие у ней углы одного треугольника равны соотвественно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны)

Доказательство:

Пусть АВС и А 1 В 1 С 1 – два треугольника, у которых АВ равно А 1 В 1, угол А равен углу А 1 , и угол В равен углу В 1 . Докажем, что они равны.

Пусть А 1 В 2 С 2 – треугольник, равный АВС, с вершины В 2 на луче А 1 В 1 и вершины С 2 в той же полуплоскости относительно прямой А 1 В 1 , где лежит вершина С 1 .

Так как А 1 В 2 равно А 1 В 1 , то вершина В 2 совпадет с В 1. Так как угол В 1 А 1 С 2 равен углу В 1 А 1 С 1, и угол А1В1С2 равен углу А1В1С1, то луч А 1 С 2 совпадет с А 1 С 1 , а В 1 С 2 совпадет с В 1 С 1 . Отсюда следует, что вершина С 2 совпадет с С 1. Значит треугольник А 1 В 1 С 1 совпадает стреугольниом А 1 В 2 С 2 , значит равен треугльнику АВС.

Теорема доказана.

3-ий признак равенства треугольников: по трем сторонам (Теорема 3.6. - Признак равенства треугольников по трем сторонам - Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны)

Доказательство:

Пусть АВС и А 1 В 1 С 1 – два треугольника, у которых АВ равно А 1 В 1, АС равно А 1 С 1 , и ВС равно В 1 С 1 . Докажем, что они равны.

Допустим, треугольники не равны. Тогда у них угол А не равен углу А 1 , угол В не равен углу В 1, и угол С не равен углу С 1 . Иначе они были бы равны, по перовому признаку.

Пусть А 1 В 1 С 2 – треугольник, равный треугольнику АВС, у которого Свершина С 2 лежит в одной полуплоскости с вершиной С 1 относительно прямой А 1 В 1 .

Пусть D – середина отрезка С 1 С 2 . Треугольники А 1 С 1 С 2 и В 1 С 1 С 2 – равнобедренные с общим основанием С 1 С 2 . Поэтому их медианы А 1 D и В 1 D – являются высотами, значит прямые А 1 D и В 1 D – перпендикулярны прямой С 1 С 2. Прямые А 1 D и В 1 D не совпадают, так как точки А 1, В 1 , D не лежат на одной прямой, но через точку D прямой С 1 С 2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.